LeetCode 问题 137 是一道有关位运算知识的题目。最佳解法可以使用 \(O(n)\) 的时间复杂度和常数的空间复杂度解决该问题。很遗憾关于本题目在中英文互联网中均没有一个很友好的解释,本文给出关于该问题的详细解释。
本题解参考了 Renpeng Fang 在 LeetCode 讨论区发布的文章。
题目翻译
给出一个非空整数数组,其中除一个元素出现一次以外,其余每个元素均出现三次。尝试找出单个的元素。
注意:
你的算法应当具有线性时间复杂度。你能否不需要额外内存来实现它?
示例 1:
输入: [2,2,3,2]
输出: 3
示例 2:
输入: [0,1,0,1,0,1,99]
输出: 99参考题解
一、问题描述
任给整数数组,除了一个元素出现 p 次外,其余任意元素均出现 k 次。找出出现 p 次的那个元素。
其中,k > 1 且 p >= 1,p%k 不为 0。
二、对于 1-bit 数的特例
为实现算法占用的存储空间与数组长度无关,我们考虑使用位运算(Bitwise Operation)将其实现,我们需要重新思考整数如何在计算机中被表示为二进制位。首先,我们来思考单个二进制位的情况。假设我们拥有一组由单个二进制数组成的数组(其中每个元素可能为 0 或 1),我们对数组中包含的 1 的个数进行计数,每当 1 出现的次数到达某一个特定值,比如 k 时,计数器返回到零然后重新开始(如果你好奇的话,这个 k 和上边题干中的 k 是相同的)。为跟踪我们遇到了多少个 1,我们需要一个计数器。假设这个计数器拥有 m 个二进制位:xm, …, x1(从最高有效位到最低有效位,请见《计算机中的字节序》一文)。对于该计数器来说,我们能总结以下至少四条特性:
- 计数器含有一个初始状态,为简单期间,其值为零;
- 对于数组中的每个输入,如果我们遇到一个 0,则计数器保持不变;
- 对于数组中的每个输入,如果我们遇到一个 1,则计数器累加一;
- 为了能够计到 k 次,我们需要
2^m >= k,因为需要m >= logk。
这里的关键点在于:计数器中的每个位(从 x1 到 xm)如何在我们扫描一遍数组时改变呢?注意我们刻意要用到位运算。为了满足上述第二条性质,我们回忆何种位运算在另一个操作数为 0 时不改变被操作数本身的值呢?是的,我们有: x = x | 0 和 x = x ^ 0。
很好,我们现在有了表达式 x = x | i 或者 x = x ^ i,其中 i 是迭代数组过程中的数组元素。那上述哪个更好呢?我们目前还不知道。因此,我们只需继续来做实际的计数工作。
一开始,计数器中的所有二进制位均置为零值,比如,xm=0,…,x1=0。因此我们需要选择一种位运算,使得计数器中的所有二进制位在遇到 0 的时候保持不变,直到遇到数组中的第一个 1 时才发生改变。当我们遇到第一个 1 时,我们有:xm=0,…,x2=0,x1=1。之后又遇到了第二个 1,我们有:xm=0,…,x2=1,x1=0。对于 x1 = x1 | i,当第二次计数的时候 x1 还会是 1。所以很显然我们应该用 x1 = x1 ^ i。对于 x2,…,xm 又会发生什么情况呢?思路是找到 x2,…,xm 将改变自身值时的情况。我们以 x2 为例。如果我们遇到了一个 1 然后需要改变 x2 的值时,x1 需要处于什么情况时我们才能做出改变呢?答案是:x1 必须为 1,否则我们不应该改变 x2,因为 x1 从 0 到 1 就已经完成了计数工作了。所以 x2 只有当 x1 和 i 均为 1 时才会改变其值,或者从数学的角度来说,x2 = x2 ^ (x1 & i)。类似地,xm 只有当 xm-1,…,x1 和 i 均为 1 时才会发生改变:xm = xm ^ (xm-1 & ... & x1 & i)。很好,我们找到了和逻辑对应的位运算。
然而,你也许会注意到上述位运算将会从 0 一直计数到 2^m - 1,而不是 k。如果 k < 2^m - 1,我们就需要某种能够当计数器到达 k 时重置计数器至 0 的“截断”机制。为此,我们在 xm,…,x1 上对所有位与一个被称作掩码(mask)的变量引用位与操作,比如,xm = xm & mask, ..., x1 = x1 & mask 。如果我们能保证掩码当且仅当计数器到达 k 值时为 0,而其他情况下均为 1 时,我们就搞定了。如何做到这一点呢?来想一想如何将计数到 k 的情形与其他情况区分开。嗯,就是计数 1 的个数!对于每一次计数来说,计数器的每一位都有独特的值,可以被看做是(计数器)的状态。如果我们用二进制的形式写出 k 值:km,…,k1,我们则可以依据以下方法来构造掩码:
mask = ~(y1 & y2 & ... & ym),当 kj = 1 时 yj = xj,而 kj = 0(j = 1 一直到 m)时 yj = ~xj。
我们举几个例子:
k = 3: k1 = 1, k2 = 1, mask = ~(x1 & x2);
k = 5: k1 = 1, k2 = 0, k3 = 1, mask = ~(x1 & ~x2 & x3);
总结起来,我们的算法应该长这样子(nums 是输入数组):
for (int i : nums) {
xm ^= (xm-1 & ... & x1 & i);
xm-1 ^= (xm-2 & ... & x1 & i);
.....
x1 ^= i;
mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).
xm &= mask;
......
x1 &= mask;
}
三、对于 32 位数字的通常情况
是时候将我们对于单个二进制位的结果推广到 32 位整数了。一个直截了当的方法是对于整数中的每一个位创建 32 个计数器。然而,如果我们能够吸纳位运算的优势,则可能将 32 个计数器“组合到一起”。“组合到一起”是在说我们用 m——一个 32 位的整数来表示 32 个 m 位的计数器,此时 m 是满足 m >= logk 的最小整数。原因是由于,位运算对于不同位上的操作彼此独立(显而易见,对吧?)。这样我们就可以将含有 32 个计数器的对应位归为一个 32 位的整数。下面是一个示意图,展示了如何做到这一点:
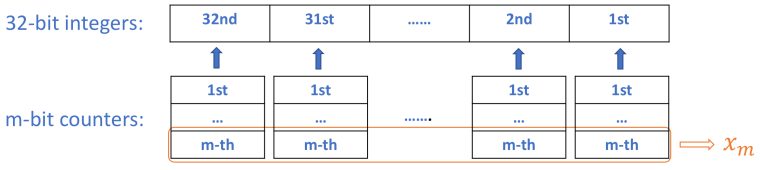
最上边一行是 32 位的整数,对于其中的每个二进制位,我们有着对应的 m 位的计数器(箭头底下的元素)。因为对于 32 个二进制位的位运算彼此相互独立,我们可以进行归整操作,也就是将所有计数器中的第 m 个二进制位,归到同一个 32 位整数中(黄色框)。在这个 32 位整数(记作 xm)中的所有二进制位将遵循统一的位运算。由于每一个计数器都含有 m 个二进制位,我们最终得到 m 个 32 位数,对应于第二部分的定义分别是 x1,…,xm,但它们现在是 32 位的整数而不是单个二进制位的数。因此,在上边的算法中,我们只需将 x1 一直到 xm 看作 32 位整数而非单个二进制的数即可。其他的一切都是一样的,我们就完成了。很简单,对吧?
四、返回何值
最后一件事情是我们应该返回何值,或者说,从 x1 到 xm 中的哪个值等于那个单个的元素。为了得到正确的答案,我们需要理解 32 位整数 x1 到 xm 都表示什么。以 x1 为例,x1 有 32 个二进制位,记作 r(r 从 1 到 32)。当我们完成对输入数组的扫描后,x1 的第 r 个二进制位的值将由数组中所有元素的第 r 个二进制位决定(更具体地说,假设数组中所有元素第 r 个二进制位的 1 的个数总和为 q,q' = q % k 且其二进制表示为 q’m,…,q’1,根据定义,x1 的第 r 个二进制位的值应等于 q’1)。现在可以问自己一个问题:x1 的第 r 个二进制位为 1 意味着什么?
该问题的答案是寻找什么能作用于这个 1 上。一个出现 k 次的元素能如此作用吗?不能。为什么?因为如果一个元素需要起作用,必须至少同时满足以下两个条件:该元素的第 r 个二进制位必须为 1,且 1 出现的次数不能为 k 的整数倍。第一个条件很好满足。而第二个条件来自于每当 1 的个数达到 k 时,计数器又会从 0 开始,也就是说 x1 中对应的二进制位被设置成了 0。对于出现了 k 次的元素来说,上述两个条件不可能被同时满足,也就是说,这种元素起作用。不过,那个只出现过 p(p % k != 0)次的元素会起作用。如果 p > k,那么前 k * [p/k] 次出现的([p/k] 表示 p/k 的整数部分)那个独特的元素都不会互相作用。所以我们可以总是设 p' = p % k,并且说那个独特的元素出现过 p' 次。
让我们把 p' 写成二进制形式:p’m,…,p’1(注意 p' < k,所以用 m 个二进制位就能装下)。这里我们快速通过底下的证明来强调 xj 等于独特元素的条件是 p'j = 1(j 从 1 到 m)。
若 xj 的第 r 个二进制位为 1,我们可以肯定地说那个独特元素的第 r 个二进制位也是 1(否则没有其他情况能令 xj 的第 r 个二进制位为 1)。我们要证明的是,如果 xj 的第 r 个二进制位是 0,那么独特元素的第 r 个二进制位也只可能是 0。假设一下在这种情况下,独特元素的第 r 个二进制位为 1 时会发生什么情况。在(对输入数组的)扫描结束以后,1 将被记了 p' 次。根据定义,xj 的第 r 个二进制位等于 p’j,也就是 1。这与 xj 的第 r 个二进制位为 0 矛盾。因此我们得出结论,只要 p'j = 1,xj 的第 r 个二进制位就与独特元素的第 r 个二进制位相同。由于这个结论对 xj 的所有二进制位均有效(r 从 1 到 32 都有上述结论),因此我们说只要 p'j = 1,xj 就等于独特元素。
那么我们现在就很清楚应当返回什么了。只要将 p' = p % k 用它的二进制形式表达出来,只要 p'j = 1,就可以返回相应 xj 中的任意一个。总结来说,该算法具有 \(O(n*\log{k})\) 的时间复杂度以及 \(O(\log{k})\) 的空间复杂度。
附注:有一个关于 xj 中的每个二进制位与 p’j 以及独特元素 s 中给的每个二进制位相关的一般公式,写作 (xj)_r = s_r & p'j,(xj)_r 与 s_r 分别表示 xj 与独特元素 s 的第 r 个二进制位。利用这个公式,容易看出当 p'j = 1 时有 (xj)_r = s_r,也就是说,只要 p'j = 1,就有 xj = s,如上所示。因此,无论独特元素的值是多少,只要 p'j = 0,就有 (xj)_r = 0,换句话说, p'j = 0 时 xj = 0。综上所述,我们有:如果 p'j = 1,就有 xj = s;如果 p'j = 0,就有 xj = 0。这也就是说表达式 ( x1 | x2 | ... | xm ) 就能得到独特数字 s 的值,因为将独特数字本身与一堆 0 进行位或运算得到的结果还是那个数字本身。
五、示例
这里是一些展示该算法如何工作的示例(再举出其他例子就很简单了):
k = 2, p = 1k为2,所以m = 1,我们只需一个 32 位的整数(x1)就能作为计数器。且2^m = k,所以我们甚至不需要掩码!一个完整的 C++ 程序应该长这样:
int singleNumber(int[] nums) {
int x1 = 0;
for (int i: nums) {
x1 ^= i;
}
return x1;
}k = 3, p = 1k为3,所以m = 2,我们需要两个 32 位的整数(x2,x1)来做计数器。并且由于2^m > k,我们需要做一个掩码。将 k 写为它的二进制形式:k = '11',因此k1 = 1,k2 = 1,所以我们定义掩码mask = ~(x1 & x2)。完整的 C++ 实现如下:
int singleNumber(int[] nums) {
int x1 = 0, x2 = 0, mask = 0;
for (int i: nums) {
x2 ^= x1 & i;
x1 ^= i;
mask = ~(x1 & x2);
x2 &= mask;
x1 &= mask;
}
return x1; // 由于 p = 1, 二进制形式是 p = '01', 所以 p1 = 1, 我们可以返回 x1.
// 如果 p = 2, 二进制形式是 p = '10', 因此 p2 = 1, 我们应当返回 x2.
// 或者我们也可以简单地返回 (x1 | x2).
}
k = 5, p = 3k为5,所以m = 3,我们需要三个 32 位整数(x3,x2,x1)来做计数器。并且由于2^m > k,我们也需要掩码机制。将k写为其二进制表示形式:k = '101',所以有k1 = 1,k2 = 0,k3 = 1,因此mask = ~(x1 & ~x2 & x3)。完整的 C++ 实现如下:
int singleNumber(int[] nums) {
int x1 = 0, x2 = 0, x3 = 0, mask = 0;
for (int i: nums) {
x3 ^= x2 & x1 & i;
x2 ^= x1 & i;
x1 ^= i;
mask = ~(x1 & ~x2 & x3);
x3 &= mask;
x2 &= mask;
x1 &= mask;
}
return x1; // 由于 p = 3, 二进制表示为 p = '011', 因此 p1 = p2 = 1, 所以我们可以返回 x1 也可以返回 x2.
// 如果 p = 4, 二进制表示为 p = '100', 则只有 p3 = 1, 说明我们只能返回 x3.
// 我们也可以简单地返回 (x1 | x2 | x3).
}
法律声明
本题解参考了 Renpeng Fang 发布于 LeetCode 讨论区中的文章《Detailed explanation and generalization of the bitwise operation method for single numbers》。如对于原文内容有侵权,请告知。