硬盘危机——Chia 挖矿背后的原理与技术细节（一）

大容量硬盘成为新的理财产品
来自 v2ex.com 上的主题讨论

近日，一种被称为 Chia 的数字资产成为最新的讨论热点。与其他主流类型的区块链上资产不同，Chia 采用了空间与时间证明（Proof of space and time）的共识算法进行资产分配。该项目声称为整个行业提供一种“环境友好的挖矿方式”，却因为造成大量硬盘缺货而被广为人知。

本文作为“硬盘危机——Chia 挖矿背后的原理与技术细节”系列的第一篇文章，介绍 Chia 特色的空间与时间证明算法，深入讨论该共识算法的原理以及技术细节，解释这种挖矿方式为何要求大容量的存储设备。本文主要参考自《Chia Consensus Algorithm》白皮书文档。

共识算法

运行于区块链上的数字资产采用各自不同的共识算法以分配资产。诸如 BTC（比特币）等资产采用了一套简单直接的工作量证明（Proof of work，PoW）方法，即通过具备大量算力的硬件计算哈希（Hash）以证明其工作量。PoW 方法的问题在于消耗了过多的能源。根据 University of Cambridge 发布的分析显示，BTC 网络一年耗费的电力超过阿根廷整个国家的用电量。此外，由于特定硬件制造的所有权以及廉价能源分布的集中，使得普通用户不容易参与 PoW 的过程，也使网络容易受到各种攻击。

另一种共识算法被称为权益证明（Proof of stake，PoS），该方法存在多种不同形式，但仍存在诸如易通过交易所集中控制资金、依赖定期与网络进行同步、以及普通用户不易参与其中等的显著缺点。

在分布式共识系统中，系统的运作依赖于特定种类的可被加密验证（Cryptographically verifiable）且稀缺（并非无限获得）的资源，以抵抗 Sybli 攻击。PoW 与 PoS 中的稀缺资源分别是计算能力与权益。而在空间与时间证明（Proof of space and time，PoST）共识算法中，Chia 采用了存储空间作为稀缺资源。由于存储空间并非无限，因此他们认为，空间证明是更加贴近于比特币最初的“一个 CPU 一票”的理想替代方案。例如，拥有 300 GiB 的用户拥有三“票”，而拥有 500 GiB 存储容量的用户则有五“票”。这里的“投票”指的是在区块链上赢得并且验证该区块的机会。

而在 Chia 的共识算法中，仅仅采用空间作为稀缺资源是不够的。因此，PoST 共识算法引入了时间作为另一种稀缺资源。该算法创建了一种可验证延迟函数，以作为时间已经被流逝的证明。通过时间与空间的结合，Chia 构造了这样一种挖矿场景：用户将数据存储在硬盘驱动器上一段时间，而赢得区块记账权利的机会与分配的空间大小成正比。该机制通过与彩票中奖类似的方式，允许所有普通用户均可参与其中，而不需要任何特殊硬件、资金以及注册才可加入。

空间证明

从概念上来讲，Chia 采用下列方法来实现对存储容量的证明：

验证者向证明者发出一项质询（Challenge），然后
证明者向验证者证明在某一时刻，验证者保留了特定数量的存储空间

空间证明的实现细节非常复杂，有兴趣的读者可以参阅这一篇文章。DGideas 博客将会在未来详细讨论该证明的理论依据。不过简言之，对空间的证明由以下三个阶段组成：标绘（Plotting）、证明（Proving，即挖矿过程），以及验证（Verifying）。

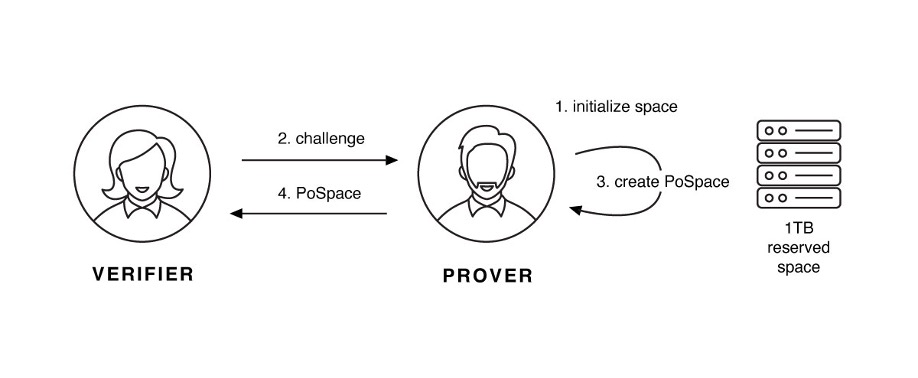
一张图示验证者和证明者是如何交互的图示。在图示中，证明者使用 1TB 保留空间。首先初始化一批空间，然后收到来自验证者的挑战，随后证明者创建 PoSpace，然后将 PoSpace 返回给证明者 — Chia 共识算法白皮书中对于空间证明的示意图，首先证明者（Prover）标绘或分配部分硬盘空间 (1). 然后通过空间证明 (2,3,4). 来响应质询以实现挖矿过程，验证者检查该证明对该质询是否有效

Plotting

标绘（Plotting）过程即硬盘容量的初始化过程。证明者（挖矿用户）是任何拥有至少 100 GiB 可用空间的人，也可能有拥有大量未使用空间的企业。存储空间容量不设上限。标绘过程可能持续几个小时到几天的时间，该过程只需执行一次。经过初始化的空间被一个称为 plot 的文件占用。绘图文件（plot 文件）的大小由参数 \(k\) 决定，其中占用空间为 \(780k * 2^{k-10}\)，而最小的 \(k\) 取值为 32，即文件大小为 101.4 GiB。

从 Chia 1.0 版本始，使用快速的商业计算机能够在六小时之内创建一张 k32 绘图文件，而对于具有单核心 CPU 以及几 GB 内存的慢速计算机来说，这个过程可能需要 24 个小时。PopSpace 的构建基于 Beyond Hellman 的这篇论文，但是嵌套了 6 次并包含较小的修改。

以 \(k=32\) 为例，经过以上操作，我们得到的 plot 文件包含七个具有随机数据的查找表，每张表中有 \(2^k\) 个条目。表 \(i\) 中包含两个指向表 \(i-1\) （上一个表）的指针。最后，每张表 \(1\) 的条目都包含一对介于 \(0\) 和 \(2^{k}\) 之间的整数，称为“x 值”。空间证明是具有一定数学关系的 64 个 x 值的集合。

一旦证明者完成了绘图文件的生成，就可以准备接受质询并创建证明。这种共识算法吸引人的一点就在于它是非交互式（non-interactive）的：创建绘图文件的过程不需要任何形式的注册或者互联网连接。类似于 PoW（工作量证明）算法，在获得奖励之前，任何人无法 Chia 修改区块链。

Proving

证明（Proving）过程旨在通过对挑战者发出一系列质询来证明他们已经按照共识中的指定方法使用了一定量的空间。当挑战者（挖矿用户）接收到质询后，他们需要检查自己的 plot 文件，生成证明，并且将任何获胜的证明提交到网络中以进行验证。

每一轮的质询过程都可以抽象为一个表查找问题。每次质询以一个 256 位的二进制序列作为输入，而期待挑战者得到一个证明作为输出结果。挑战者通过从上文所述生成的表 7 中读取一系列值以应对质询，它们指向表 6 中的两个条目，以此类推。最后，挑战者得到了整个 x 值树：该过程需要对表 7 进行一次读取，对表 6 进行两次读取，以此类推。假设用户使用的是查找时间为 10ms 的慢速机械硬盘，整个查找过程大致需要 640ms。整个过程涉及的数据量很小，且与绘图文件的大小无关。

由于此过程生成的大多数证明都不够好（下文中讨论），无法提交给网络进行验证，我们可以优化这个过程，即只检查树的一个分支，从而最终只会生成两个 x 值（而非整个 x 值树），具体取决于任务。然后，我们将以此方式生成的 x 值散列为 256 位的字符串，以确认证明是否正确。对这些 x 值进行散列处理后，我们便得到了质量字符串，即长度为 256 位的随机值。通过该值与难度系数，以及 plot 的大小相结合，可以生成 required_iterations（所需迭代次数）值。如果该值小于某一个特定数目（表示挖矿成功），那么我们就会查找整个 PopSpace。经过优化后，在慢速硬盘上查询一个分支的时间就降低到了 7 次读取与查找，即约 70ms 的时间。

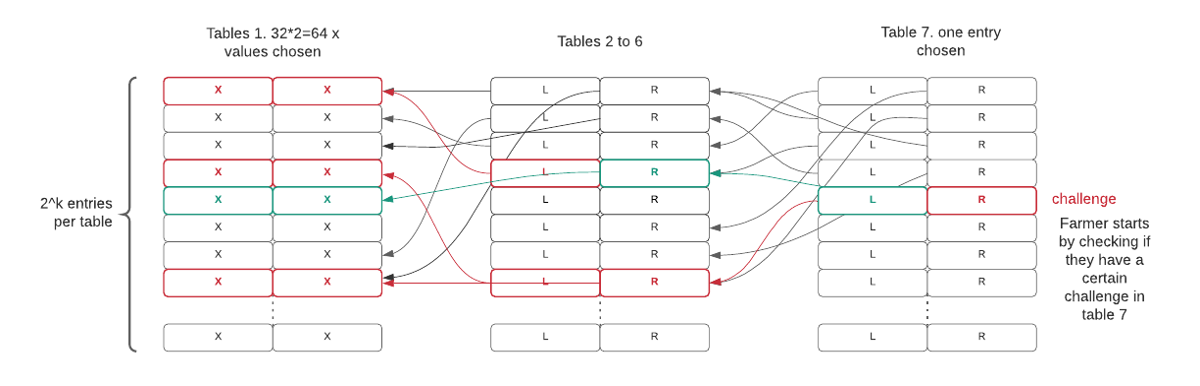
一张表示 plot 文件结构的图示，共含有 7 张表，其中每张表包含 2^k 个项目，而从表 7 中的一个项目开始向前每次双倍地查找，最终能够得到一个质量项目和 64 个证明项目 — 绘图文件的结构，64 个标注为红色的 x 值表示证明，2 个绿色的值表示质量

对于质询过程，更进一步的优化方式是使某些比例（如 \(\frac{511}{512}\)）的图不符合每个质询的要求，这种方法被称为“绘图过滤器”。举例来讲，要求质询字符串与 plot_id 以九个 0 开头。这种要求对所有人均一致（对 Replotting 攻击者除外），因此是公平的。这使得挖矿几乎不消耗任何资源，并且每分钟磁盘读取量很少。Chia 资产的用户已经使用单个 Raspberry Pi 设备实现了几个 PiB 的存储。Chia 共识算法白皮书中提到，他们假设用户使用的是廉价低速的机械硬盘驱动器，因为他们的价格比较便宜，并且由于读取速度和挖矿效率无关，所以这些用户无需使用固态硬盘。但是，可以使用固态硬盘或者内存实现更快的绘制（Plotting）过程。

Plot key 是存储在绘图文件中的私钥。而 plot ID 通过散列化绘图文件的公钥以及矿池的公钥进行签名。要创建具有空间证明的块，需要同时使用 Plot key 和 Pool key 进行签名。因此，创建绘图文件后不会对矿池产生影响。实际上，Plot key 是由 plot 中存储的 Local key 与挖矿软件中存储的 Key 通过 2/2 BLS 聚合公钥得到的。为了安全和高效，证明者可以通过此密钥和签名方案来运行集中式服务器。服务器可以连接到存储许多 plot 的“收割机”。挖矿的过程需要证明者的密钥和本地密钥，但不需要池密钥，因为可以将池的签名缓存并重用于许多区块。

Verifying

验证（Verifying）过程则简单得多，当挑战者成功地创建了空间证明之后，验证者可以通过执行一些散列操作并与证明中的 x 值相比较以确定是否证明成功。回想一下，我们已经说明证明是一个含有 64 个 x 值的列表，其中每个 x 值有 \(k\) 位长。对于 k32 来说，一共就是 256 字节长，因此非常紧凑。然而，虽然验证的过程非常快，但还不足以快到能够在 Ethereum 上（实现跨链的可靠传输）进行可靠的验证，因为验证过程需要 black3 和 chacha8 操作。

时间证明

对于时间，或者说可验证延迟函数（Verifiable Delay Function，VDF）的证明过程，实际上是对于顺序函数执行过一定次数的证明。

可验证性（Verfiable）意味着在执行计算（这需要时间）之后，证明者可以在很短的时间内创建一个很小的证明，并且验证者可以在不必重新进行整个计算的情况下验证该证明。

延迟（Delay）意味着证明者实际上花费了大量时间（尽管我们不知道确切多少）来计算函数。

函数（Function）意味着它是确定性的：在相同的输入 \(x\) 上计算VDF 总是得到相同的结果 \(y\)。

这里的关键词是“顺序性”，即意味着证明者不能仅仅通过购买更多的机器来提高运行速度，这与比特币等的 PoW（工作量证明）不同。一种要求顺序时间的方法是多次哈希：\(\mathrm{hash}(\mathrm{hash}(\mathrm{hash}(a)))\) 。因此，我们可以假设对 VDF 的计算需要消耗一定的真实时间。Chia 使用的构造是重复平方：证明者必须对质询进行 \(2^T\) 次平方，这需要 \(\theta(T)\) 的时间，证明者还必须创建证明已正确执行的证明。

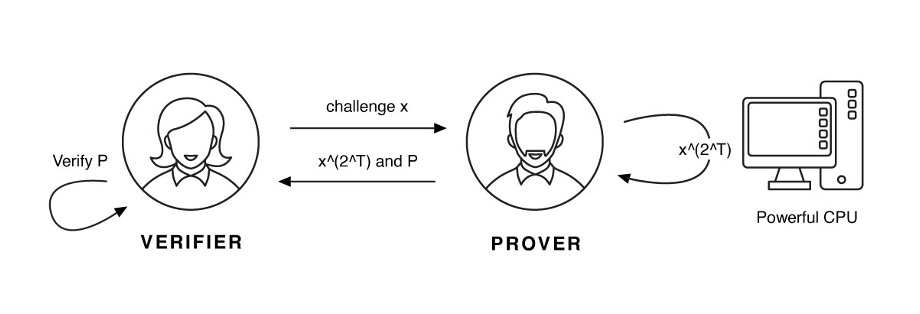
验证者向证明者发送质询 x，而证明者需要花费一些真实时间对 x 进行计算 x^(2^T) 次，并将计算结果与对该计算的过程证明 P 输出。验证者随后校验证明过程 P — 验证者（区块链）向证明者（时间领主😁）发送质询，而证明者计算输出与针对输出的相应证明

接下来所述细节对于理解共识算法并不是很重要，但是对于选择要使用的 VDF 还是很重要的。因为如果攻击者获得了速度更快的计算机，则可能仍会发生某些攻击。

Chia 使用的 VDF 是在未知顺序的类群中重复平方。生成具有未知顺序的大群主要有两种方法：第一种是使用 RSA 模数，将整数 \(\mathrm{mod}\ N\) 作为一个组。如果你采用多方计算（Multi-party Computation，MPC）形式，即在拥有许多参与方的情况下生成你的模数，那么这个组的顺序就是未知的。另一个更简单的方法是使用具有大质数判别力的类组，这就是具有未知顺序的组。这不需要任何复杂或可信的设置，Chia 采用这种方法。要创建这些组之一，只需要一个大的随机质数。缺点是类组代码在真实世界中获得的测试较少，而且优化也不如 RSA 组那样广为人知。我们使用相同的初始元素进行平方（\(a=2\)，\(b=1\) 类组元素），而根据挑战为每个 VDF 生成一个新的随机质数，作为判别子。判别子的大小为1024位，也就是说证明大小在1024位左右。我们使用 Wesolowski 方案分成\(n\)（\(1\leq{n}\leq{64}\)）个阶段，这样创建证明的速度非常快。由于 n-wesolowski 证明可能会很大，所以我们一旦有 1-wesolowski 证明就用它们来代替，因为这些证明比较小，但需要更多的时间来生成。证明本身并不体现在链上，因此它们是可以替换的。

简言之，VDF 接收一个输入，称为质询，并产生一个输出，同时产生一个证明，证明函数的评估是正确的。

将一个值注入到一个 VDF 中意味着该值与一个 VDF 的输出相结合，生成一个新的值，作为下一个 VDF 的输入/质询。因此，我们是将 VDF 串联起来，但在中间提交一个新的值（块）。这样做是为了让我们有一个块的线性进展，交替进行空间证明和时间证明。

总结

在本篇文章中，我们回顾了空间证明（Proof of space）与时间证明（Proof of time）的实现思路，并讨论了影响细节的安全问题。

读者可能注意到，我们目前仅讨论了 Chia 共识算法中所涉及的两种稀缺资源的证明方式，而仍未涉及到如何赢得并验证区块的方法。我们在后续文章中详细介绍相关细节实现。

拓展阅读

Chia 区块链的 GitHub 仓库